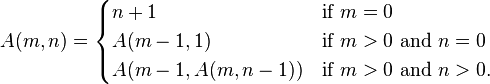My friend Rob has another excellent mathematical post up. It has, in fact, been up since December 14th, but I’m only now catching up with my starred RSS items from last month.
This post is on the nature of infinity and other large numbers, and how we mentally relate to and handle them. Here’s a taste:
[I]f you look at infinity from a size standpoint, infinity is dizzyingly terrifying. Most people don’t have a proper concept of what “large” means, but mathematicians know better:
- The universe is 13.7 billion years old, or 4.3*10^-17 seconds. Current quantum theory has trouble measuring time below Planck’s time constant, or 1.855×^-43 s. If we treat the idea of time as a discrete number of Planck’s constants, then the age of the universe is 8*10^60 of these constants. Infinity is bigger than this.
- The number of atoms in the universe is estimated to be around 10^80.
- The biggest number ever seriously used in mathematics is Graham’s number. The number is an upper bound for some mathematical property. The number is so huge that it cannot be written with scientific notation (the exponent would have more digits than atoms in the universe). Still, infinity is bigger than this number.
- The Ackermann function is a strange non primitive recursive function:
This function generates huge finite numbers. For example, A(5,2) is so large that it cannot be describing it with common math notation would take more letters than there are atoms in the universe (this includes 9^9^9^9^9^9… etc.). Still, infinity is bigger than this number.
Read the whole thing here.